如果说牛顿和莱布尼茨用微积分解锁了速度和加速度，那么17世纪末的科学家们直接撬开了曲率的秘密，推开了现代物理的大门。

故事从1673年左右开始。荷兰人惠更斯在研究摆钟时，意外发明了“曲线的“渐伸线”。

给定一条光滑曲线 C，在曲线上选取一点作为起点，把一根不可伸长的绳子紧缠曲线，保持绳子绷紧，沿曲线展开，绳端所走过的轨迹，称为曲线 C 的渐伸线（involute）。

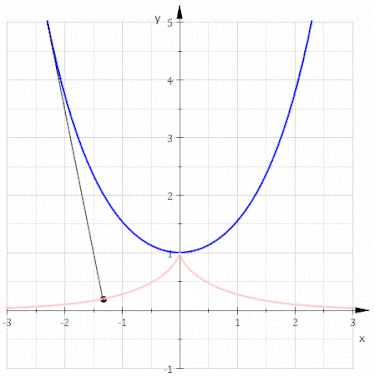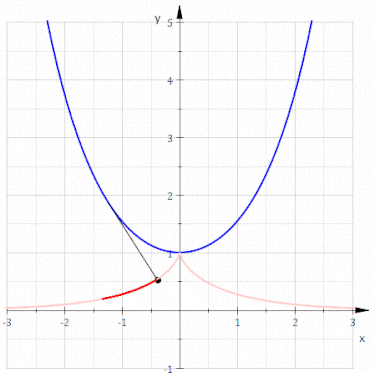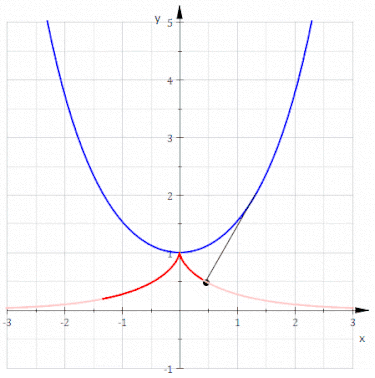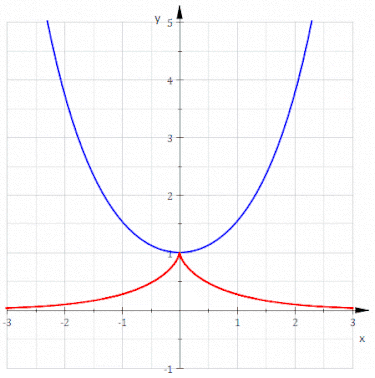
渐伸线诞生的同时，另一个概念也被孵化出来，即“曲线的渐屈线”。

给定一条光滑曲线 C，在曲线每一点作法线，相邻两点的法线交点轨迹，就是曲线 C 的渐屈线（evolute）。

从曲线上某点作法线，相邻两点的法线交点，随着点在曲线上的移动，轨迹形成了渐屈线。而且，渐屈线和渐伸线互为反演：曲线的渐伸线的渐屈线，就是原曲线本身。

惠更斯做出的物理贡献远不止数学。他发明了世界上第一批高精度钟表——摆钟，将日常误差从15分钟压缩到15秒，支撑了法国全国地形测量。法国科学院诞生，惠更斯成了首批外籍院士。

惠更斯提出了一个关键公式。给定曲线 y=f(x)，曲率半径公式为：

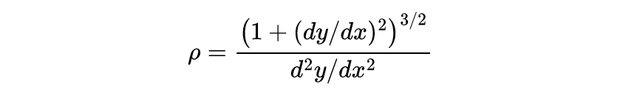
这个公式，牛顿也独立推导过。

经典例子层出不穷。摆线（cycloid），滚动圆周上定点形成的轨迹，它的渐伸线还是一条摆线，这直接被惠更斯应用到理想钟摆设计。

悬链线（catenary）是自由悬挂的链条在重力作用下形成的曲线。

曳线（tractrix）则是另一种经典曲线，满足这样的性质：在曲线的每一点，沿该点的切线向固定直线作垂线，曲线点到切线与固定直线交点的距离是一个固定的常数 a>0。

将曳线绕旋转轴旋转，可以生成一种特殊的曲面，叫做伪球面（pseudosphere），这种曲面具有常负曲率，是后来双曲几何研究的重要模型。

17世纪末到18世纪初，空间曲线的研究兴起。克莱罗和欧拉（Euler）意识到，三维空间的曲线不仅可以定义切线，还可以定义主法向量和双法向量（binormal）。每一点都有自己的“参考系”，这为后来的曲率和挠率理论奠定了基础。

到了曲面研究，欧拉的方法更进一步。他提出：在一个曲面上，取过某点及其法向量的一系列切平面，平面与曲面的交线是平面曲线。每条这样的曲线有自己的曲率，随着旋转平面，可以找到曲率最大和最小的方向，这就是主曲率（principal curvatures），分别记作k_1 和 k_2。

不同于曲线，曲面在一个点的曲率有两个基本方向，并且它们的符号可能不同。比如马鞍点，一个方向是正曲率，另一个方向是负曲率。

真正让曲率成为数学地基的人是高斯（Gauss）。

高斯一生涉猎极广，从构造17边形到数论巨著《算术研究》，再到预测小行星轨道。他在曲面研究上的工作，最终以《卓越定理》（Theorema Egregium）为高峰，系统揭示了高斯曲率的内在性。

高斯发现，k_1与 k_2的乘积，即高斯曲率（Gaussian curvature），只依赖于曲面内在的测量，和外部空间无关。

球面上，高斯曲率是正的，且为 1/ρ^2，其中 ρ是球半径；伪球面上，高斯曲率是负的，但数值处处相同。这种只依赖内部几何的量，第一次把“内在”和“外在”彻底分开，为黎曼几何和广义相对论奠定了基础。

黎曼（Riemann）接过高斯的火炬，把曲率推广到任意高维，提出了曲率张量、黎曼流形。几乎没人能完全读懂他的论文，但有一个人看懂了。

爱因斯坦。

爱因斯坦在1915年发布广义相对论。核心思想是：质量让时空弯曲，物体在弯曲的时空中沿着测地线运动。用的正是黎曼在19世纪中叶抽象出的数学工具。

今天的黑洞、引力波、宇宙膨胀，背后都是曲率在支撑。曲率，不仅描述了手中的摆线，也塑造了宇宙的骨架。