在19世纪初，数学界出现了一种新的几何体系，它不同于欧几里得两千年来主宰人们空间观念的传统框架。这就是非欧几何。

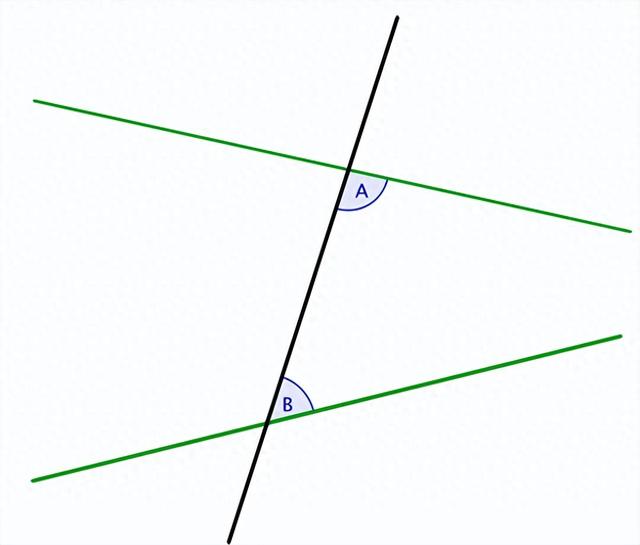
问题的源头在欧几里得《几何原本》的第五公设，即平行公设。它声称：在一条直线外的一点，可以且仅可以作一条与这条直线平行、不相交的直线。相较于其他四条公设的简洁性，第五公设显得冗长和不自然。自古以来，数学家们不断尝试用其他公设推导出第五条，却始终未果。

19世纪初，卡尔·弗里德里希·高斯通过严密的逻辑分析，首次明确意识到第五公设可能无法从其他公设推导而来。他认识到，可以构造一种与欧氏几何内部逻辑一致，但否定第五公设的新几何体系。出于当时学术环境对传统权威的敏感，高斯选择将研究结果保留在私人通信中，未公开发表。

与此同时，约翰·鲍耶和尼古拉·洛巴切夫斯基，分别在匈牙利和俄罗斯，独立发展出了这种新的几何体系。他们设想，给定直线外的一点，可以作不止一条不与原直线相交的直线。基于这一新假设，他们推导出一整套自洽的几何定理，其中包括三角形内角和小于180度、不存在大小不同但形状相同（即相似而不全等）的三角形等性质。

尽管理论自洽，非欧几何在当时几乎未被主流数学界接受。鲍耶在向高斯汇报成果时，收到高斯一封含糊地声称“早已知道”的回信。鲍耶因此深受打击，逐渐淡出数学研究。洛巴切夫斯基则在资源有限的喀山大学继续推进自己的工作，但传播范围有限，影响力一度微弱。

事实上，早在非欧几何被系统构建之前，人类已有接触非欧几何现象的经验。球面几何，即地球表面的几何结构，早在希腊、印度和阿拉伯天文学中得到了充分应用。球面上的直线为大圆，非对跖两点有唯一的大圆连接，而对跖点则有无数大圆通过。球面三角形的内角和总大于180度，并且面积与角和超出180度的部分成正比。

如果从现代眼光审视，球面几何完全可以被归入非欧几何范畴。然而，历史上受限于对《几何原本》的高度尊崇，这一事实被忽视了数百年。

非欧几何理论真正走向具体化，要归功于意大利数学家尤金尼奥·贝尔特拉米。他提出，球面方程x²+y²+z²=1描述的是正曲率空间，而如果改为x²+y²−z²=常数，则描述的是负曲率空间，即双曲面。在这种曲率为负的空间中，可以建立一种与球面几何镜像对称的新体系。

为了更直观地理解这种几何，贝尔特拉米引入了两个重要的平面模型：

这两个模型共同展示了双曲几何丰富而自洽的结构。特别是在庞加莱模型中，三角形的内角和总小于180度，并且缺失部分面积与三角形面积成正比，正如在球面几何中超出部分面积与面积成正比一样。

在双曲几何中，空间并非像欧氏空间那样线性扩展。向单位圆盘边缘前进时，距离视觉上趋向于边界，但在几何意义上，需要无限时间才能真正到达。单位圆盘的边界并不属于空间的一部分，而是作为理想界限存在。

双曲几何在镶嵌理论（tessellation）中展现出远超欧氏几何的丰富性。在欧氏平面上，只有正三角形、正方形和正六边形可以无限铺满，而在双曲平面上，可以根据需要设计出无限多种规则多边形的铺砌方式。只要每个顶点周围多边形的内角之和小于360度，即可无限展开。

20世纪，数学家哈罗德·考克斯特系统化了双曲几何的镶嵌理论。与此同时，艺术家莫里茨·埃舍尔在与考克斯特交流后，基于庞加莱模型，创作了著名的《圆极限》系列图像，将无限扩展压缩进有限空间，展示了双曲空间的视觉特性。

非欧几何不仅在数学内部引发深远变革，还对物理学产生了直接影响。阿尔伯特·爱因斯坦在构建广义相对论时，正是基于非欧几何的思想，提出时空曲率由物质和能量分布决定。空间和时间不再是绝对、恒定的背景，而是可以弯曲和变化的实体。

在20世纪初，随着黎曼几何、克莱因几何、庞加莱群论的逐步发展，非欧几何被纳入更广泛的数学体系，成为现代数学、物理学基础结构的重要组成部分。

非欧几何的建立不仅解答了一个关于公设独立性的问题，更重要的是，它提供了一种新的思考方式：通过改变基本假设，探索完全不同但内部一致的数学世界。这一突破不仅扩展了数学的边界，也深刻改变了人类对空间、结构与逻辑一致性的基本理解。