这篇说小学求阴影面积的题目

01

拉窗帘

小学几何常见难题是求“阴影部分面积”。

阴影部分通常又是三角形。

（圆和不规则图形，属于中学部分，提前考是小升初内容，你懂的）

这个三角形总不让你轻易知道底和高。

不好算了。

于是，你就看到网上刷屏的“拉窗帘”模型。

所谓拉窗帘模型就是：

两条平行线之间夹的三角形，只要底不变，无论顶点如何移动，面积都不会变。

因为，平行线之间的距离是一定的。

利用这一点可以在求阴影面积的题目中“大展拳脚”——

小学生的“阴影面积求值”多在正方形中进行；而正方形，有两对平行线。

明白这点，遇到求阴影面积：

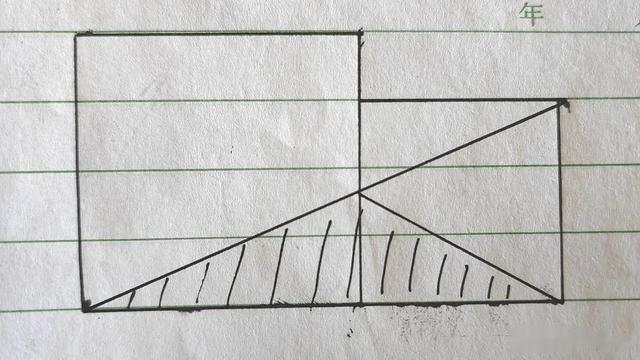
孩子们要先找平行线和三角形的底边；找到后，把平行线所夹的三角形沿着平行线来回“拉动”；然后把不规则的三角形“拉”到规则位置；这样三角形的面积（阴影部分的面积）就呼之欲出了。

比如下面这道题。

让我们计算红色阴影部分的面积。

乍一看不好算。

运用拉窗帘模型：

找到大正方形的平行线、找到三角形的底边。把不好算的面积1和2部分，转移到3和4部分。接下来，根据边长，就能轻松解答。

是不是感觉很利落、畅快？

是，我也觉得挺好——高效解题的爽感谁都想要。

然而，值得注意的是：

这是高手总结出来的模型，像这样的模型很多，掌握多了，的确能够快速解题。但模型虽好，我们不能被它框住，要理解背后的本质，才能以不变应万变。

那么，本质就在“等积变换”4个字里。

02

等积变换

三角形的面积公式是s＝½ah。

a是底，h是高。

等积就是等面积，要使三角形面积相等，有很多种情况：

最简单的，底相等、高相等；来点变化，底乘高相等。

底和高可以不相等——底可以扩大，高可以缩小。

记住这点！

遇到求阴影面积，刻意去找一找面积相等的部分，题目也被你快速解出。

举个例子。

下图如果用拉窗帘的方法是：

找平行线、把三角形变换到合适位置、求解。

而等积变换是：

看看有没有办法把不好算的阴影部分转移一下。那么转移要么等高等底转移，要么乘积相等转移。在正方形里，通常都是等高等底转移。

那么，找到相同的底和高就行了。

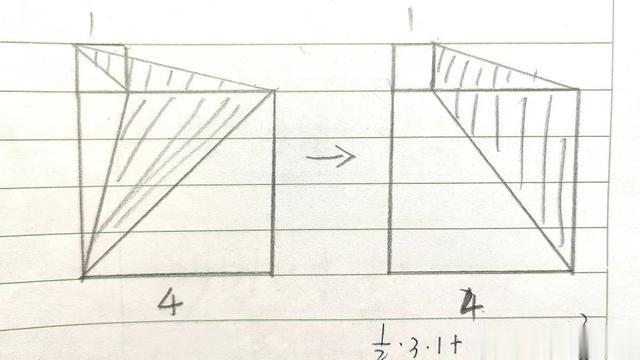
两种方法，其实不差什么。

“拉窗帘”也没有更便捷，只是更好记——也给不知道如何等积变换的孩子提供了一个抓手。

但不要依赖它。

因为，在数学中我们更应该重视的是【定性分析】。

等积变换属于【定性分析】——

它是从概念出发延伸的方法。

在数学中有定量分析也有定性分析，定性分析是要在定量分析前面的。

也就是要从概念出发，接近更本质的东西，这样可以触达更多。

比如下面这道题，是初中数学的内容。

那么，我们也能拉窗帘吗？

显然不好使了。

这时候我们要用等积变换。

先看，菱形，遇到这种特殊四边形，你首先要把对角线连一连。

因为所有的几何题，本质上都在算位置关系和数量关系。

而特殊四边形的对角线：

互相平分（平行四边形）、

互相垂直（菱形）、

互相垂直且相等（正方形）、

相等且互相平分（矩形），

有这么多关系，为何不连？

一连，立马找到一对面积相等的三角形。

然后，你再把EC连起来。

为啥不连？

辅助线普通人不可能一下子看出来，见点就连一连，试一试，准没错。

一连，又出现了面积相等的三角形。

然后，再利用面积比来计算边长比，利用边长比来计算面积……

就是这样：

通过找面积相等的三角形，不停变换；最终把所有空白部分的三角形面积都计算出来；题目可解了。

解题步骤，我写在下图中。

你看，求阴影面积，等积变换是关窍，而非“拉窗帘”。

可以说拉窗帘是快捷方式，但是如果你总依赖快捷方式，格局就打不开。

要用更本质的东西去解题，这样才能触类旁通。

谢谢阅读，本文结束

欢迎点爱心、转发。