01

我们的计算

我们的计算很统一，无论加法、减法、还是乘除都列竖式。

其中加减法和乘法竖式，个别规则不同，但形式挺统一的。

这样的统一形式，能够减轻小孩子的认知负担。

让孩子在初级计算方面，能够快速切换、学习概念时能够形成体系。

然而速度不够快。

你会发现到两位数，三位数之后，孩子已经在脑子里倒腾不过来了，需要在纸上笔算。

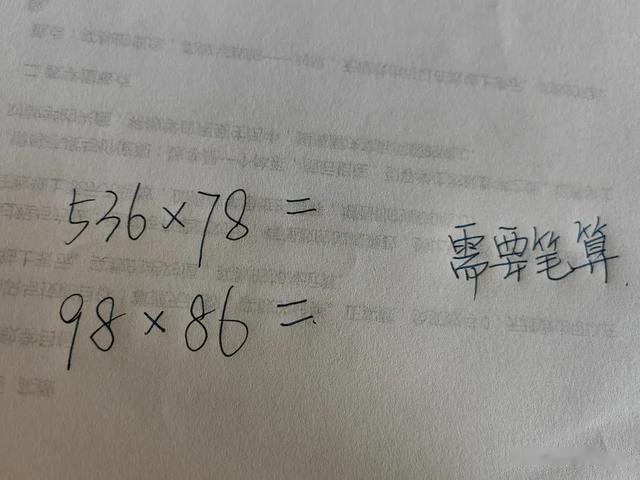
在两位数之前，甚至包括两位数，孩子都可以心算出来，在卷面上的速度相对来说还是挺快的。

大数速度慢了，好多家长就很恐慌。

其实你不用恐慌。

到大学，甚至高中，就可以用计算器了。

在中考和高考中，不需要三位数的计算，都是一位数、小数和分数的计算，基本上没有超过两位数的计算。

你会看到中考或者高考的卷子，很长的一个式子，最后得出来的得数很小。

02

最快还是珠心算

所以不用恐慌。

但如果你真的很想让孩子算的更快一点，可以学一下珠心算。

珠心算，学会了之后就是“闪电速度”，算的非常快。

但也不是速成的，得练。

一般孩子都不想练，也没必要逼的孩子“痛不欲生”。

似乎印度计算“很热”，有家长说学这个行不行？好像也挺快的。

甚至有人鼓吹印度计算厉害，比中国小学生的算式强多了。

我带大家看看。

不可否认，阿三的数学能力还是很强的。

但不见得比我们快。

下面我给大家演示一下。

03

印度计算方法

加法计算：

他们是先算有几个百，再算有几个十，然后再算有几个“个”。

之后加在一起就能得出正确答案。

如果按照这样的计算方式算，刚开始学加法，还不太熟练的小学生，是可以直接写答案的，这时候看起来比我们的竖式要快一些。

当然，熟练后用我们的十进制进位法也是可以直接写答案的，在加法上熟练之后速度上没有太大区别。

在乘法上区别稍微大些。

下面我们来看看。

他们是先算有几个百，然后是算有几个十，然后再算有几个“个”，之后加在一起，跟他们的加法实质其实差不多。

把我们的竖式和他们的，写在一起对比，你就会发现他们的是比较长的。

但是呢，如果你熟练了之后，这个是很容易心算化的，你就可以直接写答案——因为都是整数，加起来比较容易。

也就是说你不用列竖式。

不过这只限于两位数，最多到三位数。数位再大，就不行了。

数位大，还是竖式方便一些。

04

工具化

为了更方便，更具体，印度就把这种计算方法固定成了工具——划线算点。

比如，32×21=672

因为是三个十斜着画三条线，然后再在对面平行着画21里面两个十的两条线。（如果是3位、4位，就多画几排线）

然后再反方向画32里2的两条线，上面画21里的1，一条线，最后数点数，直接写答案。

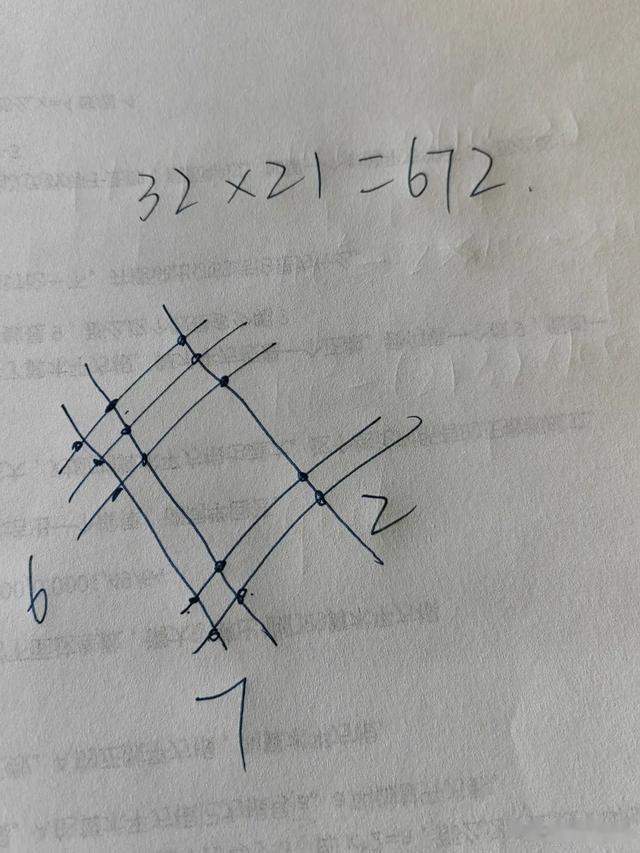
有人可能觉得这样还没我们的竖式快，但是如果遇到三位数、四位数的乘法，这个方法显然会更慢一些。

正确率也不见得高。

不信你可以试试，3578×9976=？

如果用竖式，要乘4次，再加4次，牵扯到很多进位，很容易出错。

而用印度这种划线的方法，则……更容易出错。

05

为什么

那他们为什么这么算呢？

其实他们是用了初中学的多项式求和公式，把数字分解当成多项式。

分解后，把百位部分、十位部分、个位部分相加。

他们把这些百位、十位、个位都拆分到竖式里边或者还有这种横线的点上面，其本质上，还是多项式相乘，并且不违背乘法是加法计算的初衷。

这种分解法在有规律的数字乘法方面会更方便。

比如计算平方数。

可以利用多项式相乘的计算方法，很把乘方运算转化成整数相乘，很快的得出答案。

还有比较接近100的数。

看看每个数跟100差几个。

比如97，跟100差3，98跟100差二2，那么就可以直接写答案：

就是一万里边减掉3+2个百，再加上2×3=6就是9506。

这些可以作为拓展，给孩子讲讲，当个新知识。

然而，就速度而言，没必要再学这一套了。

而且我们的竖式已经足够应付初等数学的所有计算了。

这就是的看法了，如果你有不同意见，欢迎留言分享。