在教育测评领域，掌握度评估正从“分数导向”走向“认知建模”。本文以IRT（项目反应理论）为核心，系统解析其建模逻辑、参数含义与应用场景，帮助产品人理解如何通过数据驱动实现更精准的知识评估。

一家优秀的在线教育企业，除了在商业模式上具有一定优势外，其核心还是教育质量与效果，传统评估教育质量与效果是通过做题正确率、学习时长等参数作为教学效果的体现，但这样的做法比较粗糙，存在很大的误差。项目反应理论（IRT）作为教育效果测量领域的核心模型，通过量化学生能力与题目特性的关联，为在线教育知识点掌握度评估提供更加精准、科学的解决方案。本文将从公式推导、参数意义、应用场景三个维度，对IRT模型进行深度解析。

一、IRT模型的公式推导

IRT模型的推导建立在一系列核心假设之上，这些假设是模型有效性的基础，同时也决定了其在在线教育场景中的适用边界。

1.核心假设

单维性假设：

假设学生对某一知识点的作答表现，仅由“该知识点的掌握能力”这一单一潜在特质决定，不受其他无关因素（如答题情绪、外界干扰）等影响。这一假设贴合在线教育中“针对性评估单一知识点”的需求，例如评估学生对“一元二次方程求根公式”的掌握度时，仅聚焦该知识点的能力维度。

局部独立性假设：

学生对不同题目（同属同一知识点）的作答反应相互独立，即对一道题的作答结果不会影响另一道题的作答。在线教育中，同一知识点的题库设计常遵循此假设，避免题目间存在逻辑关联导致评估偏差。

特征曲线假设：

学生答对某道题的概率，随其知识点掌握能力的提升而单调递增，即能力越强，答对概率越高，这一关系可通过“项目特征曲线（ICC）”呈现。

2.IRT公式

IRT公式一共有以下参数：θ(学生能力值/知识点掌握度)、题目区分度a(能够区分学生能力强弱)、题目难度b()、题目猜测参数c(能力为0也可以猜对的概率)，根据参数数量可分为1PL模型（Rasch模型）、2PL模型、3PL模型，在线教育中常用双参数与三参数模型。3PL模型的公式如下：

P(θ)：此习题的答对概率；

D（常数1.702）：用于校准概率尺度，使Logistic模型与正态卵形模型（Lord模型）近似，提升计算效率。

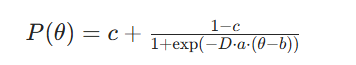
1.学生能力参数θ

θ是IRT模型的核心输出，直接对应学生对某一知识点的掌握度，具有以下关键意义：

精准量化与横向对比：θ的取值（[-3，3]）可将“掌握度”从模糊的“会/不会”转化为精准的数值。例如，学生A的θ=1.2，学生B的θ=0.5，说明A对该知识点的掌握度显著高于B，且差值可量化，避免传统“正确率相同但能力不同”的偏差（如A答对难题，B答对易题，正确率均为80%，但θA>θB）。

动态追踪能力变化：在线教育中，可通过学生在不同时间点的θ值，追踪其知识点掌握度的提升或下降。例如，学生在课程开始时θ=-0.3，课程结束后θ=1.1，说明教学有效提升了其掌握度，为教学效果评估提供直接依据。

2.题目难度参数b

题库难度梯度划分：将题目按b值分为“基础题（b≈-1）”“中档题（b≈0）”“难题（b≈1）”，匹配不同θ值的学生。例如，对θ=-0.8的新手学生，推送b≈-1的基础题，避免因题目过难导致挫败感；对θ=1.5的进阶学生，推送b≈1的难题，满足其提升需求。

知识点难度校准：通过大量学生的作答数据，计算某一知识点下所有题目的平均b值，可判断该知识点的整体难度。例如，“微积分导数应用”的平均b=1.2，“小学数学加法”的平均b=-1.5，为课程设计（如“微积分”需更多课时）提供参考。

计算方式（经典测量理论）

最常用“通过率（P值）”表示(，P=答对该题的学生人数/参加测试的总学生人数

P取值范围：(0=b时，P(θ)>0.5，能力越强概率越高；当θ