[LG]《Opal: An Operator Algebra View of RLHF》M Gaikwad [Microsoft] (2025)

Opal 提供了一个全新的算子代数视角，系统化刻画强化学习中的人类反馈（RLHF）目标函数，揭示其结构与等价关系。

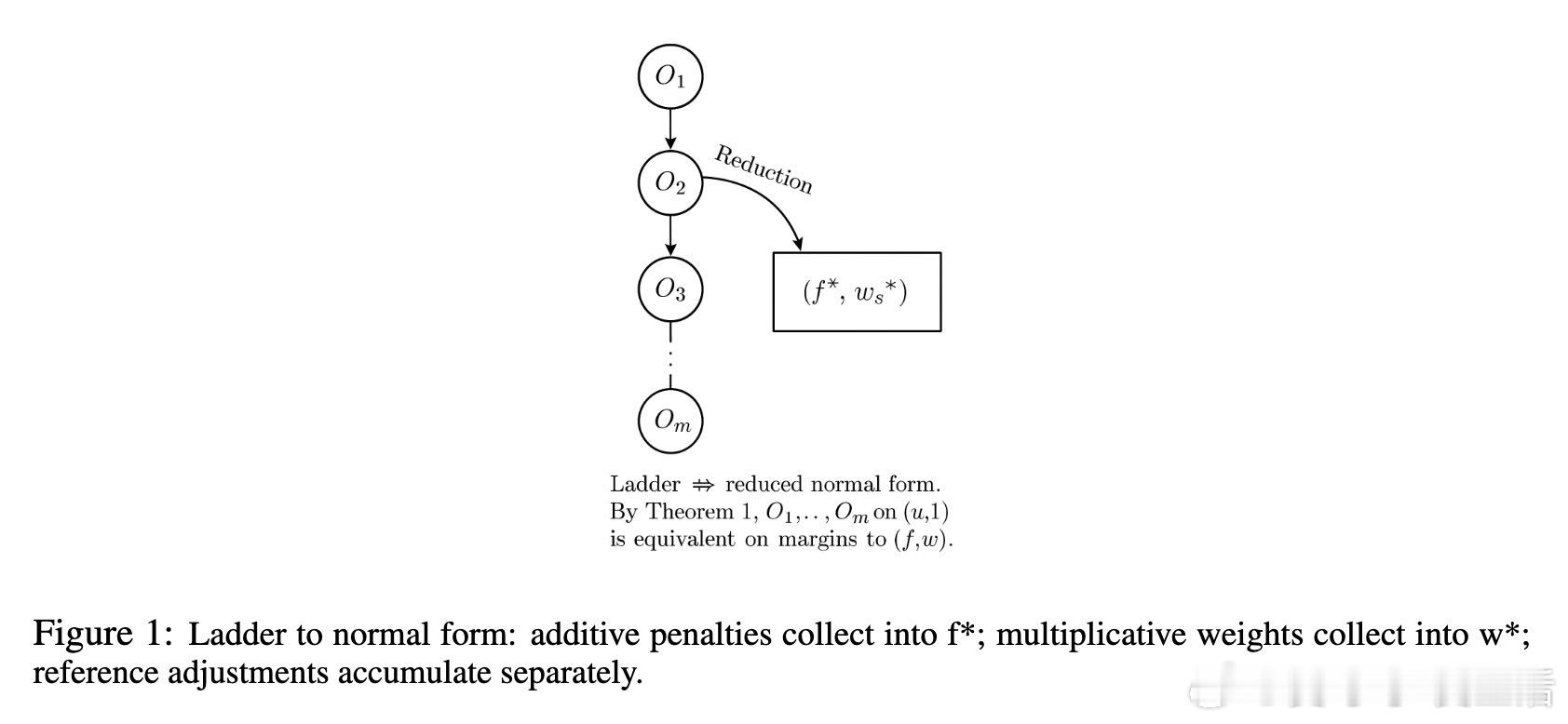
• 目标用基准分数上的“梯子”表达：由加法罚项（penalties）与乘法权重（weights）两种原语算子构成，分别调整分数与成对边际（pairwise margin）。

• 归约定理（Theorem 1）指出：当且仅当满足三大条件——固定参考（reference）、罚项可加性、权重与中间边际独立时，目标函数可化简为唯一的标准形式（normal form），确保决策等价。

• 三大非归约失败模式：参考偏移变化（reference shift）、非加性门控（non-additive gating）、得分依赖权重（score-dependent weights），均有具体有限反例证明不可归约。

• GKPO（Generalized Kernel Preference Object）作为统一的 JSON 规范，编码任意 RLHF 目标，支持归约形式的规范化与哈希，显式标记非归约原因及相应反例，促进方法间无损转换与透明验证。

• 通过 GKPO 展示了 DPO、RRHF、ORPO 等主流方法的算子结构与相互转换，设计了应对 SHIFT/GATE/SCORE 三种压力测试的验证机制，附带 Python 参考实现便于复现与集成。

心得：

1. 复杂多样的 RLHF 目标本质上可通过加法与乘法算子组合统一描述，揭示了多种方法在决策层面的本质等价，极大简化了对比和复现难度。

2. 固定参考和算子可加性是保持目标函数归约性与稳定性的关键，偏离这两点即引发不可避免的行为差异，提供了理论界与实践界辨识方法间本质差异的利器。

3. GKPO 的规范化与哈希机制为 RLHF 领域带来了类似软件工程中的版本控制与审计能力，推动了研究成果的标准化报告和可审计性，降低了重复实验成本。

详细阅读👉 arxiv.org/abs/2509.11298

强化学习人类反馈算子代数机器学习模型对齐