这篇我们说面积的基础

所有面积公式，都源自于边长为1的小正方形。

01

回忆

回忆一下课本教给我们的第一个面积公式：

矩形（长方形）的面积s=ab.

其中，a和b分别是矩形的长和宽。

课本引导我们：

把矩形分成面积是1厘米的正方形小块；然后算一算矩形里有多少这样的小块；有多少个，矩形面积就是多少。

接着，我们来到了正方形面积。

同理，s=ab,只是这里，a=b。

平行四边形的面积，我们可以利用割补三角形的方法来求出。

如下图，割补后，是不是得到了一个矩形？

只不过这里的ab，换成了底乘高。

而三角形的面积则是½ah。

最好理解的方式是:把一个正方形裁成两个相等的直角三角形。

按照同样的思路，我们来到平行四边形。

画一个平行四边形，可以把它分成两个相等的三角形。或者反过来，拿任意两个全等三角形，可以拼成一个平行四边形。

后一条，是个很重要的考点。

小学生的课本上有，在题目中也会出现。

比如：

四年级下册学三角形和平行四边形时，课本会让孩子们拼一拼。

我孩子在拼的时候，只看出了梯形，我就给她剪了全等的三角形让她试。

最终，她得出结论：

两个全等的三角形（两个全等的梯形）能拼成平行四边形。

练习题中也有类似的概念辨析。

这个时候不妨给孩子讲讲：

为什么全等的三角形或者梯形可以拼成平行四边形。

因为：

平行判定——内错角相等两直线平行。全等就意味着对边相等，有一组对边平行且相等的四边形是平行四边形。

到这里，为什么梯形面积是【（上底+下底）x高÷2】，你应该可以看明白了。

（上底+下底＝平行四边形边长

x高不用解释。

÷2正好是一个梯形的面积）

小学的面积公式，也就这些了。

这些公式的推导大都以矩形面积公式为基础；而矩形面积公式，又源自边长为1厘米的正方形。

在这里，边长为1厘米的正方形是基准。

那么，它何以成为基准？

02

最初的最初

其实，给小学生讲解面积时借用的小正方形，来自于面积的定义。

面积，表示一个平面图形或物体表面的大小。在数学中，面积通常用平方单位来度量，例如平方米、平方厘米等。在欧氏几何中，单位面积就是指一个边长为1的正方形的面积——

只不过有时候是边长是1米、有时候是1厘米、有时候是1毫米。

也就是说：

单位面积本就是指边长为1的小正方形。

它是面积的衡量尺度。

现在闭环了。

只是还有一片阴云：

我们上面说的都是规则图形。

不规则的图形呢？

也可以用正方形来衡量。

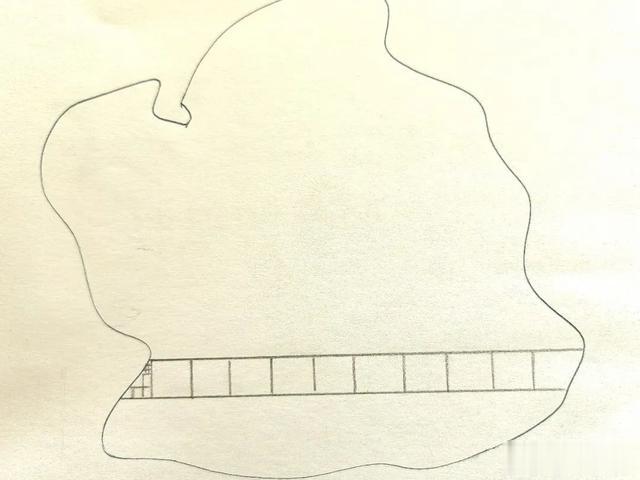
比如，一个曲曲绕绕的图形。

在这本绘本里，我看到了微分思维

怎么衡量？——切分。

大的地方我们用单位是1厘米的正方形；小的地方我们用单位是1毫米的正方形；再小我们用单位是1微米的超小正方形……

就这样无限切分下去。

看出来没有？计量单位就是这么来的。

1米不能衡量比它短的长度，就把1米分成10分米；

1分米再分成10厘米，1厘米分成10毫米……

于是，我们也有了小数。

这也是微积分的思想。

很早很早以前，三角形、四边形、甚至多边形的面积，古人就能算了。

多边形只要边是平滑的，大不了多分几个三角形嘛。

不平滑的，就要想办法了。

还是切分。

如下图：

把不规则图形，用矩形来近似；我们可以把它切分成很多超小的矩形；超小的矩形又是由超小的正方形组成的。

正是利用这种思想，天才的阿基米德计算出了圆的周长、面积和表面积。

下面链接是拓展阅读。

圆的面积，球的表面积、体积公式，是怎么推导出来的？

03

后来的后来

想必你是看出来了：

不是人人都是阿基米德。让我们每个人都去逼近，算个普通的面积还行，弯弯绕绕的肯定能算傻。

别担心，自有大神替你负重前行。

来到牛顿和莱布尼茨的时代，它们各自独立发明了微积分。

把逼近，加和的过程推导出一个固定公式——微积分基本公式就这么诞生了。

就是下图这个公式。

用它来算面积，十分好用。

可以说，它是计算面积最好的、最方便的公式。

原则上，一个合格的高中生要会使用它。

我们举个例子。

下图中两个函数所围成的面积，不好算。

我们把两个函数当成导函数，找出它们的原函数。

然后代入基本公式，答案就出来了，so easy！

通常这样的题在高考中是一个5分的填空题。

再看一个题目。

有了微积分基本公式，我们就不用割补、切分了，圆的面积只需要演算。

这种演算，平时也会让高中生训练。

出现在高考中，日常必须训练，意思很明显：

不会逼近没关系，有现成的公式，得会使用。

就像发明电脑对你来说很难，但别人发明出来，我们学会用还是相对容易的。

这也是大多数数学家的目的：

找到更多的数学模型、数学工具，方便大家使用。

那么，我们的小正方形就是工具之一，也是面积的起源。

起初它用来算普通面积，后来它被应用于推导微积分基本公式。

看，在工具的基础上又迭代了其他工具。

数学就这么交织着，走到今天。

总结：

小学期间的面积公式依赖于矩形；矩形面积公式则是由单位正方形推导而来；单位正方形还在逼近法中，用来衡量不规则图形的面积；基于这个工具，又跳到了微积分基本公式。

工具里，蕴藏着数学思维。

数学思维并不高深，无非是你能不能用工具解决数学问题。

数学里有许多小工具，而数学又是一类工具的统称。

请记住这些。

下次你再去看数学概念的时候，会有许多新发现。

谢谢阅读，本文结束。