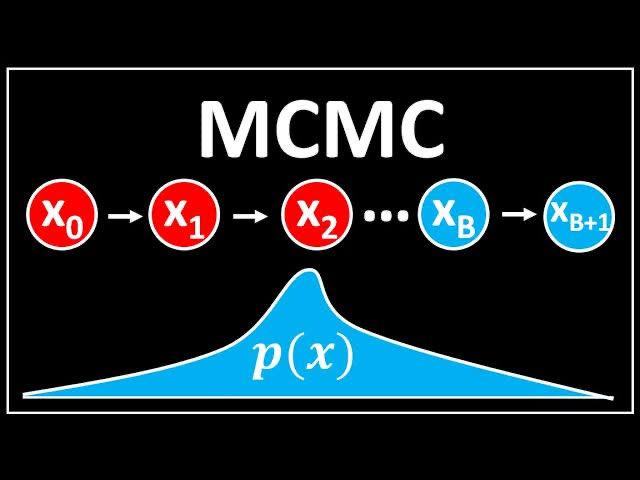
你走的路，每一步都算数？ 你相信吗？这句鸡汤背后，其实隐藏着一个强大的统计学原理——马尔可夫链蒙特卡洛(MCMC)。 我们先来想象一个画面：你被蒙上眼睛扔进一个陌生房间，任务是摸清所有家具的位置，并画一张房间地图。你会怎么做？ 大概率是这样：随机地迈出小步，如果碰到东西，就记住它的位置；没碰到就继续探索。 随着时间推移，你对房间布局就会有个大致了解。 这个看似简单的策略，和MCMC的核心思想非常相似。让我们拆解一下： - 蒙特卡洛：它代表着通过大量随机抽样来解决问题。你不知道家具在哪，所以选择随机探索，希望通过大量的随机尝试来逼近真相。 - 马尔可夫链：它的特点是未来的概率分布只取决于当前的状态，与过去的历史路径无关。下一步怎么走，只取决于你现在所处的位置，而和你之前走过的所有路径没有关系。 MCMC方法就是巧妙地将蒙特卡洛的随机性与马尔可夫链的“无记忆性”结合起来。 在统计学和机器学习中，我们经常需要估算一些未知参数（比如复杂模型的最佳设置），这些参数共同构成了抽象的“参数空间”。 MCMC方法会让计算机在这个“参数空间”里进行随机“游走”。它不会直接计算出精确的最优解，而是在这个空间里不断地随机采样。 当它“走到”某个区域时，会根据一定的规则（通常是基于目标分布的概率）来决定下一步是留在当前区域，还是跳到另一个区域。 MCMC能“暴力”解决许多无法直接计算的复杂问题。它不预设答案，只定义好探索的规则。通过生成数百万个可能的“解”（也就是采样点），出现频率最高的那个“解”，就是MCMC给出的最佳答案。 从蒙眼画房间到预测未来，MCMC启示我们：有时候，答案不需要“精确计算”，只需要“聪明地乱走”。 就像创业、恋爱、学新技能——多方向撞墙，记录有效路径，答案自会浮现。