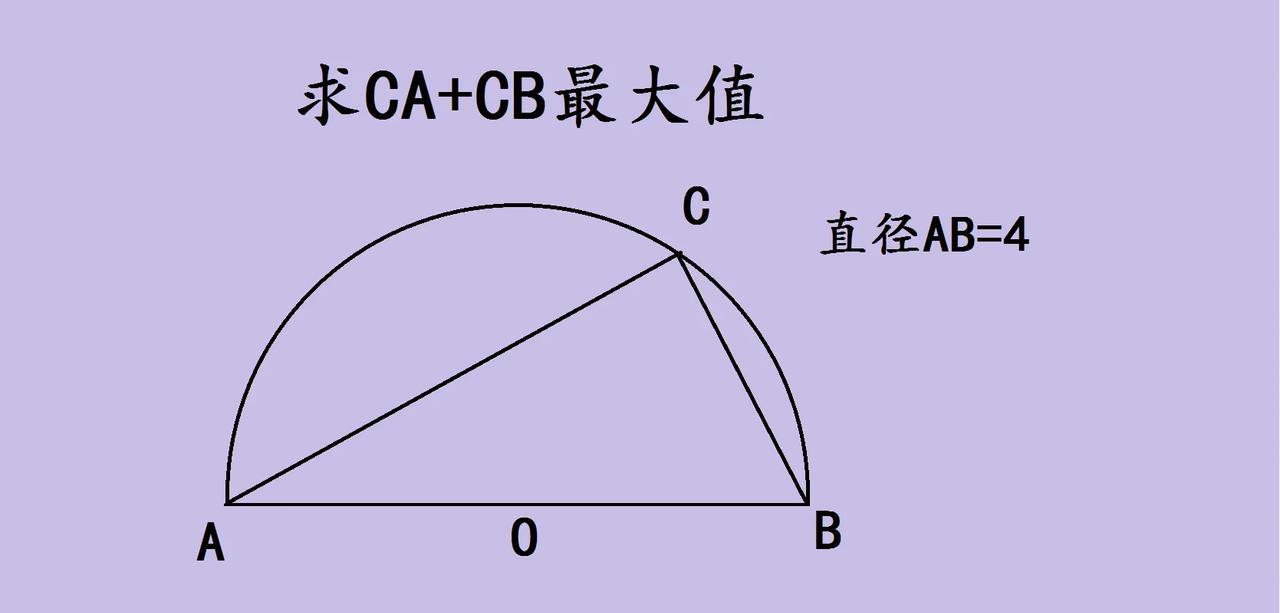
半圆上找最值，几何思维太奇妙 今天碰到个超有意思的几何题，半圆AB直径长4，点C在半圆弧上，求CA + CB的最大值 。这得调动圆的性质和几何最值思路呀！ 首先，AB是直径，根据圆周角定理，∠ACB肯定是直角，三角形ABC是直角三角形。那CA + CB的最大值咋找呢？或许可以用代数方法，设CA、CB长度，结合勾股定理（CA2 + CB2 = AB2 = 16 ），再利用完全平方公式变形，找和的最大值；也能靠几何变换，比如把其中一条线段翻折，构造新线段，利用两点之间线段最短或者三角形三边关系来突破。 几何题的魅力就在于把这些定理、性质串联，从不同角度尝试，像解谜一样。这道题把直角三角形和半圆结合，找线段和的最值，逼着咱发散思维，用代数或几何变换的招儿。探索过程超有成就感，仿佛打开几何世界新大门，大家也快来感受这种奇妙的思维碰撞呀，一起解锁几何最值的奥秘～