利用图形解代数不等式证明题 图一是一道代数不等式证明题,直接计算比较麻烦,一般常用构图法解决 如图二,作正方形,边长为a+b+c,其对角线AC=√2(a+b+c),折线AC=√(a²+b²)+√(b²+c²)+√(c²+a²)。根据两点之间线段最短可得: √(a²+b²)+√(b²+c²)+√(c²+a²)≥√2(a+b+c),显然a=b=c时,等号成立。
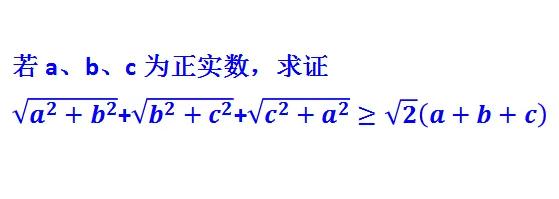
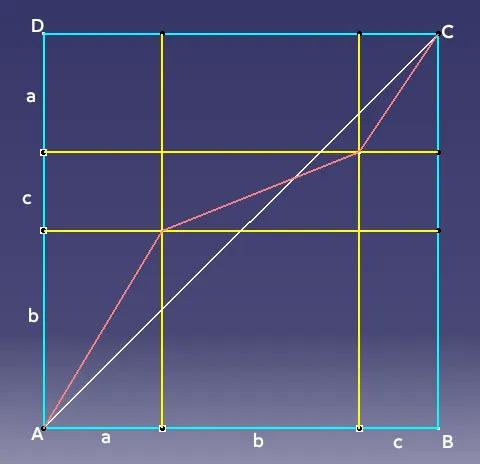
利用图形解代数不等式证明题 图一是一道代数不等式证明题,直接计算比较麻烦,一般常用构图法解决 如图二,作正方形,边长为a+b+c,其对角线AC=√2(a+b+c),折线AC=√(a²+b²)+√(b²+c²)+√(c²+a²)。根据两点之间线段最短可得: √(a²+b²)+√(b²+c²)+√(c²+a²)≥√2(a+b+c),显然a=b=c时,等号成立。
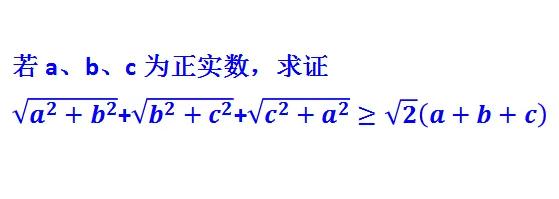

评论列表